Основы модальных испытаний и анализа

Материалы компании Crystal Instruments
под редакцией Олега Туркалова,
представителя компаний Crystal Instrumetns
и Sentek Dynamics в России
Перевод: Артем Вахитов

Метод модального анализа (определение собственных частот и форм (мод) собственных колебаний) — важное средство изучения вибрационных характеристик механических конструкций. Суть его в том, что сигналы вибрационного возбуждения и измеренные сигналы отклика сложной конструкции, трудные для непосредственного восприятия, преобразуются в набор легко прогнозируемых модальных параметров. Физико-математическая подоплека этого метода непроста, но с помощью приведенных здесь теоретических сведений и примеров можно легко уяснить его основную идею и способы применения.

Модальное представление

Модальное представление, или представление собственных колебаний, — один из возможных способов рассмотрения вибрации конструкций. Вибрация и деформации конструкций при механическом возбуждении на собственных частотах характеризуются конкретными формами, которые называются собственными формами колебаний (колебательными модами). В типовых условиях эксплуатации характер вибрации будет сложным, включающим все собственные формы. Но если изучить каждую собственную форму отдельно, то с помощью этих знаний можно анализировать все имеющиеся типы вибрации. Кроме того, в ходе модального анализа сложная конструкция, которая трудно воспринимается в своей целостности, преобразуется в набор простых для понимания независимых систем с одной степенью свободы. Определение собственных частот, коэффициентов демпфирования и форм колебаний конструкции по результатам измерений частотной передаточной функции (ЧПФ) называется модальным анализом.

Например, свободно опертая балка, возбуждаемая на первой собственной частоте, деформируется в соответствии с первой (V-образной) собственной формой колебаний (рис. 1). В этом случае балка совершает двунаправленное циклическое перемещение из положения, показанного сплошной линией, в положение, представленное пунктирной линией. При возбуждении на второй собственной частоте деформация балки соответствует второй (S-образной) собственной форме колебаний. Если же возбуждение происходит на частоте, находящейся в промежутке между первыми двумя собственными частотами, деформация соответствует некоторой суперпозиции первых двух собственных форм. Третья собственная форма колебаний балки напоминает букву W. Чем выше номер собственной формы колебаний, тем больше узловых точек наблюдается.

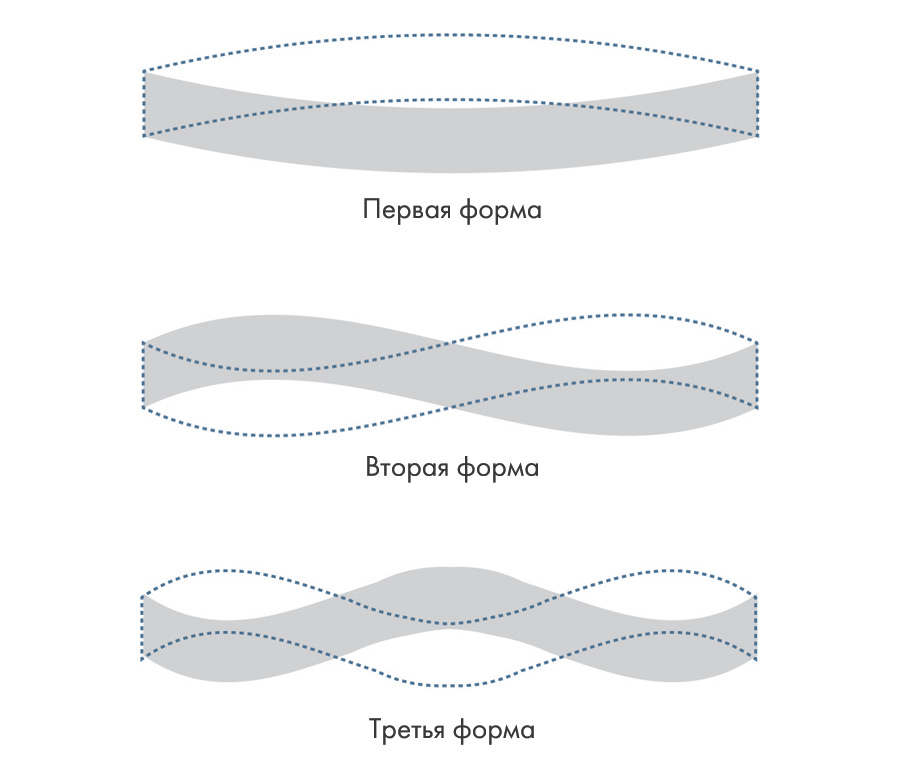
Рис. 1. Собственные формы колебаний свободно опертой балки

Для прогнозирования вибрационных характеристик проектируемой конструкции можно использовать динамический анализ методом конечных элементов. При таком анализе всю конструкцию представляют теоретически в виде набора пружин и масс, после чего можно составить систему матричных уравнений, описывающих конструкцию. Затем к полученным матрицам применяется математический алгоритм для определения собственных частот и форм колебаний конструкции. С помощью этого метода прогнозируют модальные параметры конструкции до ее изготовления, чтобы заблаговременно выявить возможные проблемы и устранить их на ранних стадиях процесса проектирования.

Далее, построив конструкцию или опытный образец, можно путем экспериментального модального анализа определить (подтвердить) фактические модальные параметры. Экспериментальный модальный анализ заключается в возбуждении конструкции некоторым способом и измерении ее ЧПФ во всех узловых точках расчетной сетки. Пример очень простой конструкции — вилочный камертон (рис. 2). Если измерить его ЧПФ в различных точках, результаты будут выглядеть так, как показано на этом рисунке. Собственные частоты индицируются пиками, возникающими на одной и той же частоте в каждой точке конструкции. Амплитуда пика в каждой точке описывает собственную форму колебаний на данной резонансной частоте, а острота пика показывает степень демпфирования каждой собственной формы.

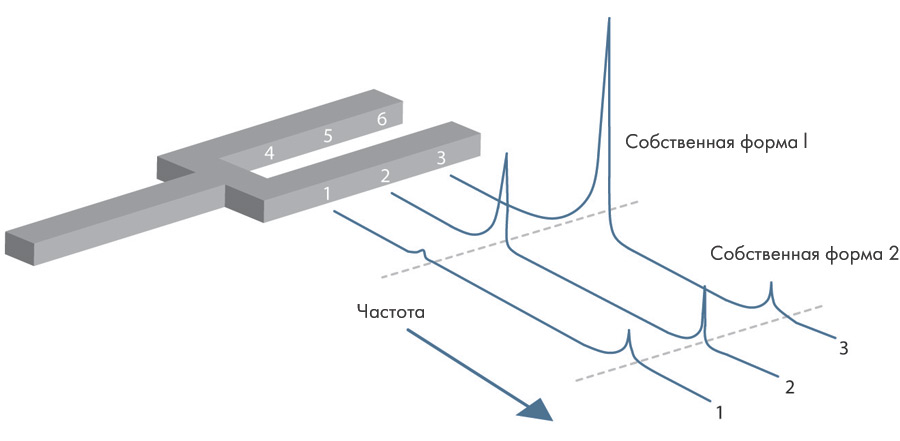
Рис. 2. Результаты модального анализа вилочного камертона

Приведенные на рис. 3 результаты показывают, что в случае первой собственной формы основание камертона зафиксировано, а конец его претерпевает максимальную деформацию, показанную на рисунке. Вторая собственная форма имеет максимальное отклонение в середине камертона.

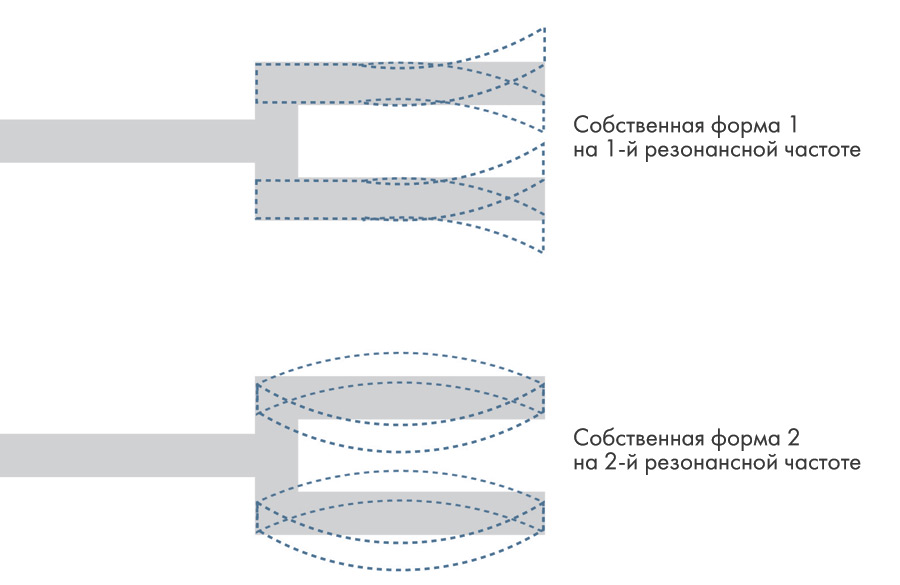
Рис. 3.1. Первая и вторая собственные формы колебаний вилочного камертона

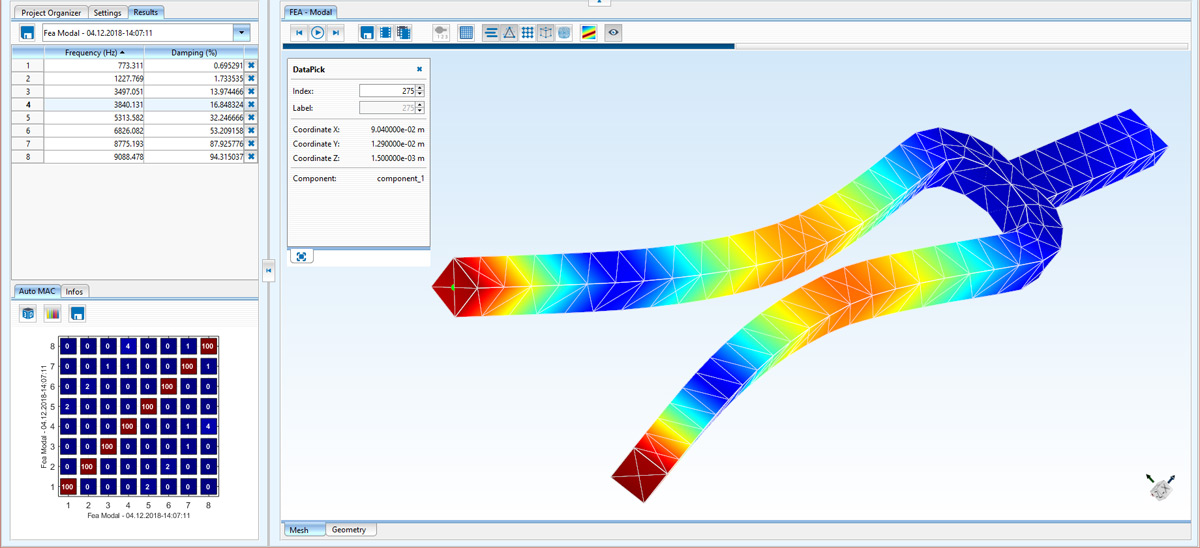
Рис. 3.2. Программная визуализация второй моды камертона

Применения модального анализа

Собственные формы и частоты конструкции, называемые для краткости «модальные параметры», можно прогнозировать с помощью математических моделей, построенных методом анализа конечных элементов. Такая модель состоит из дискретных точек, соединенных между собой элементами, чьи математические свойства соответствуют характеристикам материалов конструкции. В модель вводятся граничные условия, задающие способ крепления конструкции к основанию или ее расположения на опорах, а также приложенные к ней нагрузки. К построенной модели применяется математический алгоритм, с помощью которого определяются собственные формы и частоты колебаний. Эти данные помогают инженерам проектировать конструкции и выяснять их вибрационные характеристики еще до изготовления. На рис. 4 показана конечноэлементная модель космического летательного аппарата с действующими на него нагрузками и граничными условиями.

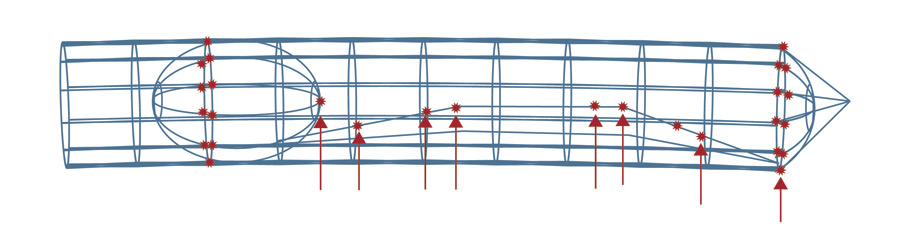
Рис. 4. Конечноэлементная модель космического летательного аппарата

После того как конструкция изготовлена, полезно проверить ее конечноэлементную модель методом экспериментального модального анализа. Сопоставление результатов этого анализа с теоретическими предсказаниями по конечноэлементной модели позволяет выявить и скорректировать ошибки в модели. Экспериментальный модальный анализ можно выполнять и без анализа по методу конечных элементов — просто для определения модальных параметров и, следовательно, вибрационных характеристик уже изготовленной конструкции.

Модальный анализ служит важным средством выявления и устранения проблем, связанных с вибрацией конструкций. Одна из распространенных проблем такого рода, которую позволяет обнаружить модальный анализ, — взаимодействие функции возбуждения с собственной частотой конструкции. В этом случае любое возбуждение, обусловленное, например, разбалансировкой вращающихся частей автомобильного двигателя, возвратно-поступательным движением в машине, широкополосным шумом ветра или дорожным шумом в транспортном средстве, заставляет конструкцию вибрировать, создавая как банальный дискомфорт для водителя и пассажиров, так и реальную угрозу движению. Функцию возбуждения можно проанализировать в частотной области для определения ее спектрального состава. Когда частота возбуждения совпадает с собственной частотой конструкции, результатом может стать очень сильная вибрация конструкции, что чревато ее усталостью и отказом.

С помощью модального анализа определяют собственные частоты, коэффициенты демпфирования и формы собственных колебаний конструкции. Если становится известно, что частота возбуждения совпадает с одной из собственных частот, определенных в ходе модального анализа, конструкцию можно пересмотреть в целом или скорректировать таким образом, чтобы отодвинуть ее собственную частоту от частоты возбуждения. В частности, можно дополнить конструкцию элементами жесткости, увеличить или уменьшить ее массу — тогда частота возбуждения более не будет совпадать с собственной частотой конструкции. Эти методы применимы для отстройки собственных частот от частоты вынуждающей силы. К другим методам виброзащиты относится повышение степени демпфирования конструкции за счет смены материала или покрытия поверхности конструкции вязкоупругим материалом. Конструкция может оснащаться динамическими виброгасителями, настроенными на частоту вынуждающей силы. В таком случае сильная вибрация возникает в самих виброгасителях, а вибрация конструкции ослабляется.

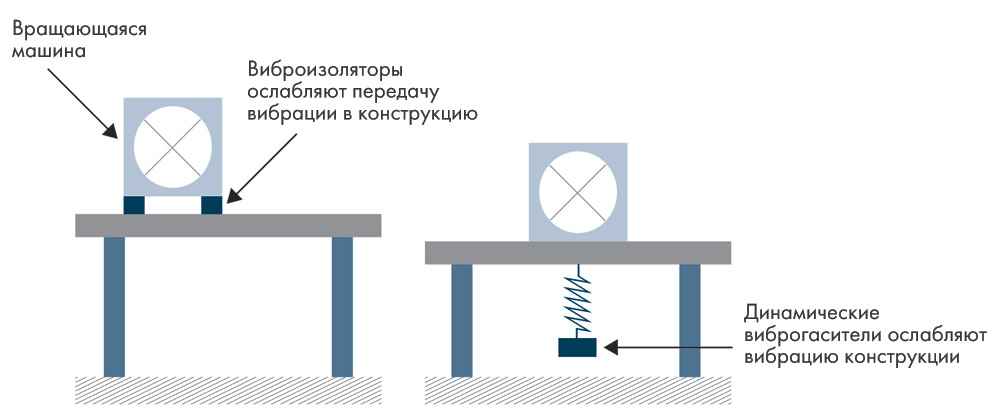
Рис. 5. Виброизоляция (слева) и динамическое гашение вибрации (справа) — методы пассивной виброзащиты

Если эти методы недостаточно эффективны, может применяться активная виброзащита, когда вибрация измеряется датчиками и по результатам измерений компьютер вырабатывает задающий сигнал для исполнительного механизма, противодействующего вибрации конструкции.

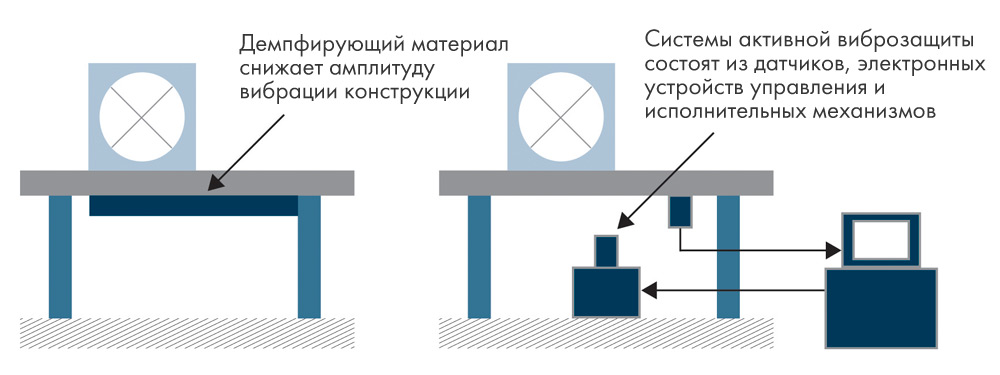
Рис. 6. Самый распространенный метод виброзащиты — демпфирование, самый дорогостоящий — активная виброзащита

Какой бы метод виброзащиты ни применялся, модальный анализ обычно служит отправной точкой для определения собственных частот, коэффициентов демпфирования и собственных форм колебаний конструкции. Модальные параметры помогают выявить причины нежелательной вибрации и найти действенное решение.

Регистрация данных для модального анализа

Первый этап экспериментального модального анализа — измерение возбуждения и отклика исследуемой конструкции. В конструкции возбуждается вибрация, после чего измеряются вынуждающая сила и вибрационный отклик конструкции (обычно виброускорение), и таким образом регистрируется набор данных ЧПФ. По этому набору данных можно определить модальные параметры, в том числе собственные частоты, коэффициенты демпфирования и собственные формы колебаний. Затем можно визуализировать собственные формы колебаний в анимационном виде.

Для того чтобы получить вибрационный отклик, необходимо возбудить вибрацию в конструкции. Есть два самых распространенных средства возбуждения вибрации: ударный молоток и модальный вибростенд. Ударный молоток, изображенный на рис. 7, — специализированное средство измерения, с помощью которого вызывается кратковременное возбуждение конструкции путем удара по ней в некоторой точке (рис. 8). Молоток оснащен тензодатчиком, вырабатывающим сигнал напряжения, пропорциональный вынуждающей силе. Так измеряется вынуждающая сила в ходе испытания. Ударный молоток часто используется для модального анализа простых конструкций или в случаях, где применение модального вибростенда нецелесообразно с практической точки зрения. Устанавливая на молоток ударные наконечники различной твердости, можно менять диапазон измерительных частот ударного воздействия. При необходимости выполнения измерений на низких частотах используется наконечник из мягкой резины, а на высоких частотах — из твердого металла.

Рис. 7. Ударный молоток, оснащенный тензодатчиком с наконечниками различной твердости

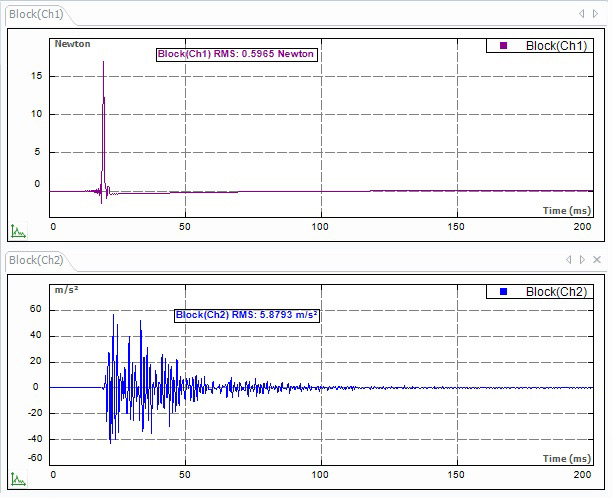
Рис. 8. Сигналограммы силы воздействия ударным молотком (input1) и отклика конструкции (input2)

Для лабораторных модальных испытаний часто используется модальный вибростенд. Такие системы характеризуются вынуждающей силой, которую они вырабатывают, и имеют разные размеры. Как правило, в режиме гармонической вибрации номинальная вынуждающая сила модальных вибросистем находится в диапазоне от десятков до сотен ньютонов. Выбор размера модального вибростенда зависит от вынуждающей силы, необходимой, чтобы получить достаточный уровень отклика от исследуемой конструкции.

Рис. 9. Модальные вибростенды используются при лабораторных измерениях и различаются по своим размерам

Обычно вибростенд соединяется с исследуемой конструкцией небольшим тонким металлическим стержнем, или штоком. В точке приложения вынуждающей силы к конструкции крепится тензодатчик, соединенный с одним из концов штока, — с его помощью измеряется вынуждающая сила. Довольно часто в точке приложения вынуждающей силы также крепится акселерометр для измерения виброускорения. Это легко осуществить с помощью импедансной головки (совмещенные тензодатчик и датчик ускорения).

Роль задающего генератора для вибростенда нередко играет цифро-аналоговый преобразователь (ЦАП) динамического анализатора сигналов — электронное устройство, вырабатывающее сигналы с точно заданными параметрами, которые затем усиливаются и преобразуются в сигналы возбуждения. Есть целый ряд типов профилей сигнала возбуждения: чисто случайный (белый шум), случайно-импульсный, псевдослучайный, случайно-периодический, ЛЧМ (импульсный ЛЧМ) и так далее.

Сигнал случайного профиля инициирует случайное возбуждение в широком диапазоне частот. При исследовании случайной вибрации в процессе регистрации данных можно применять оконные функции и усреднение. Одно из преимуществ случайной вибрации — возможность запрограммировать ее профиль таким образом, чтобы распределить энергию по всему спектру и тем самым оптимизировать измерения вибрации. На рис. 10-1 показаны сигналограмма случайной вынуждающей силы и вибрационного отклика (виброускорения), полученные в ходе модальных испытаний.

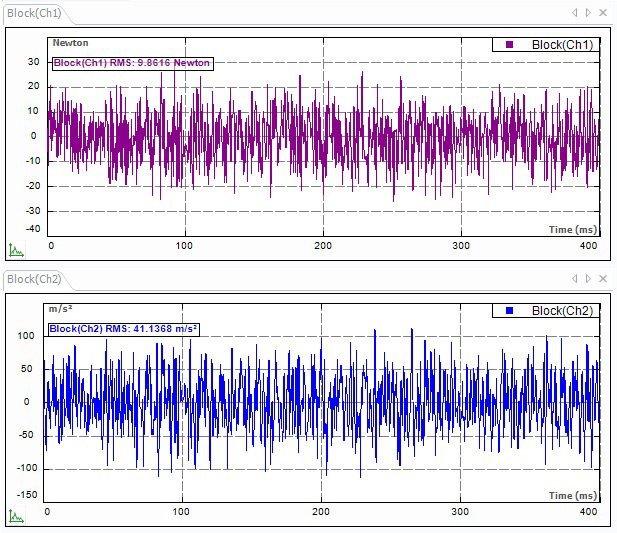
Рис. 10.1. Сигналограммы возбуждения вибрации случайным сигналом и вибрационного отклика, полученные в ходе модальных испытаний на модальном вибростенде

Случайно-импульсный сигнал состоит из двух чередующихся временных интервалов, на первом из них возбуждается случайная вибрация, а на втором возбуждение отсутствует (пауза). Длительность обоих интервалов можно программировать так, чтобы вибрация конструкции затухала к окончанию паузы. Преимущество здесь в том, что не требуется применять оконные функции, поскольку возбуждение и отклик имеют периодический характер. Случайно-импульсное возбуждение в отличие от чисто случайного позволяет гораздо точнее измерять амплитуду отклика и коэффициент демпфирования.

Псевдослучайный сигнал — это эргодический сигнал, частотный спектр которого содержит только составляющие, кратные частотному инкременту БПФ (Δf). Спектр данного сигнала имеет единичный форм-фактор с постоянной амплитудой вдоль всей оси частот, но рандомизированной фазой. Хотя случайно-периодический сигнал также является эргодическим и содержит только составляющие, кратные частотному инкременту БПФ, в его частотном спектре случайно распределены как фаза, так и амплитуда.

При использовании случайных сигналов двух указанных выше типов, если оставить достаточно времени (то есть достаточное количество циклов задержки) в ходе измерения для затухания переходных процессов от начала каждой порции сигнала, получившиеся временны́е развертки входных воздействий и реализаций отклика системы будут периодическими относительно периода выборки. Для однократного усреднения спектра сигнал во временной области, полученный из вышеупомянутого частотного спектра, повторяется (Nd + Nc) раз. Первые Nd повторов делаются в расчете на периодический отклик конструкции, а следующие Nc откликов измеряются и циклически усредняются (временно́е усреднение). Использование обоих типов случайных сигналов позволяет получить более достоверный «линейный эквивалент» конструкции, за что приходится платить значительно большей длительностью испытания.

ЛЧМ-сигнал — это короткий (обычно длительностью в 1 с или менее) синусоидальный сигнал, частота которого увеличивается по линейному закону. По достижении конечной частоты может следовать пауза, затем сигнал повторяется, и так далее. Длительность паузы можно запрограммировать так, чтобы отклик конструкции гарантированно затухал до окончания каждого временного промежутка. Тем самым обеспечивается периодичность сигналов возбуждения и отклика в пределах каждой временно́й выборки. Преимущество этого типа сигнала в том, что он создает возбуждение на всех частотах и имеет периодический характер — это избавляет от необходимости применять оконные функции, если только время выборки в анализаторе сигналов синхронизировано с ЛЧМ-сигналом. Кроме того, его характеризует более высокое отношение сигнал-шум по сравнению со случайным возбуждением. Типовые сигналограммы возбуждения конструкции импульсным ЛЧМ-сигналом и вибрационного отклика показаны на рис. 10.2.

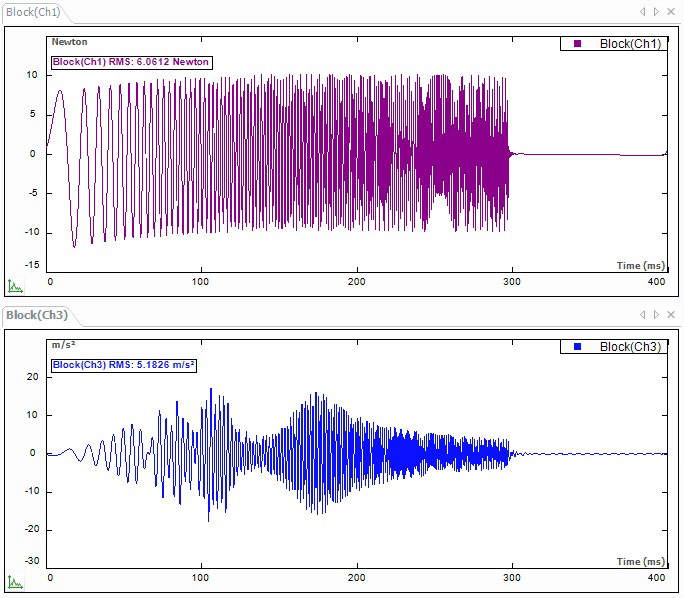
Рис. 10.2. Сигналограммы возбуждения вибрации импульсным ЛЧМ-сигналом и вибрационного отклика, полученные в ходе модальных испытаний на модальном вибростенде

Измерения: ЧПФ, функция когерентности, спектр мощности

Возбудив вибрацию в конструкции, необходимо далее измерить как само возбуждение, так и отклик. Обычно для этого на исследуемой конструкции крепят тензодатчики и акселерометры, чьи выходные сигналы регистрируются с помощью динамического анализатора сигналов. Акселерометр — это электронный измерительный датчик, преобразующий электрический сигнал в ускорение. Существуют одно- и трехосевые акселерометры. Трехосевой акселерометр в действительности представляет собой три акселерометра, ориентированные перпендикулярно друг к другу. Он обеспечивает измерение вибрации по всем трем пространственным осям. Динамический анализатор сигналов — это прибор, который регистрирует сигналы и измеряет их параметры, после чего вычисляет представление таких сигналов в частотной области.

Важный параметр при регистрации данных для модального анализа — потребное количество контрольных точек на исследуемой конструкции. Если точек слишком много, результатом будет чрезмерно большой объем данных и лишняя трата времени. Если точек недостаточно, то конструкция не будет представлена надлежащим образом и есть риск не запечатлеть искомые собственные формы колебаний. Понадобится определенное инженерное здравомыслие, чтобы оценить вероятные собственные формы колебаний и выбрать такое количество точек, которое будет адекватно представлять исследуемую конструкцию.

Наиболее распространенные типы функций, используемых в модальном анализе, — это амплитудно-фазовая частотная характеристика (АФЧХ) (иначе — частотная передаточная функция, ЧПФ) и функция когерентности. По линейным спектрам можно рассчитать спектр мощности и взаимный спектр мощности. Чтобы ослабить влияние шума, производится усреднение по множеству результирующих БПФ. Оценку ЧПФ типа H1 можно рассчитать по данным зависимости Gyx от Gxx.

Амплитудно-фазовая частотная характеристика

АФЧХ рассчитывается по двум сигналам: выходному сигналу отклика и входному сигналу возбуждения. ЧПФ описывает отношение одного сигнала к другому в представляющем интерес диапазоне частот. Она используется в модальном анализе, где измеряется ответное виброускорение конструкции относительно вынуждающей силы, воздействующей на нее при возбуждении ударным молотком или модальным вибростендом. Измеренный сигнал ЧПФ является комплексным и имеет две составляющих: либо амплитуду и фазу, либо вещественную и мнимую части. На рис. 11 показана типовая ЧПФ, представленная в логарифмическом масштабе в виде амплитуды и фазы (ЛАФЧХ).

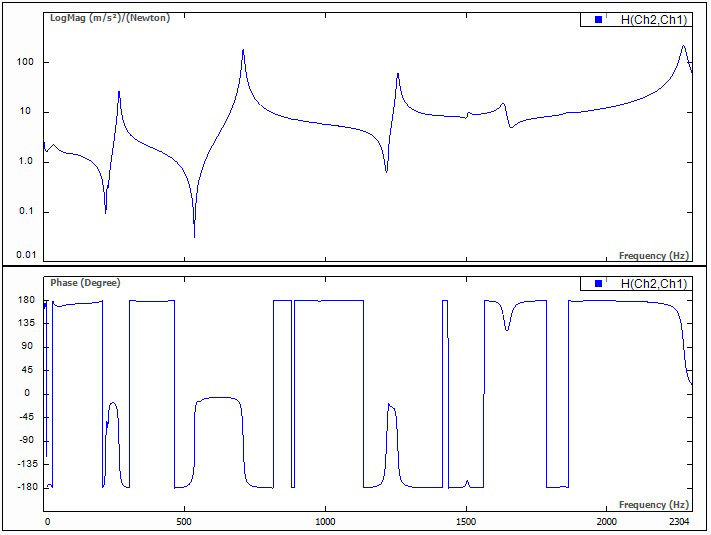
Рис. 11. Амплитудно-фазовая частотная характеристика (АФЧХ): верхний график — амплитуда, нижний — фаза

Функция когерентности связана с ЧПФ и показывает, какую часть отклика можно приписать возбуждению. Это функция частоты с областью допустимых значений от нуля до единицы. В модальном анализе по сигналу функции когерентности оценивается качество измерения. При качественном возбуждении вибрационный отклик идеально коррелирует с вынуждающей силой, о чем говорит близкое к единице значение функции когерентности во всем диапазоне частот. Функцию когерентности следует контролировать в процессе регистрации данных, чтобы обеспечить их корректность. В целом функция когерентности должна принимать значения, близкие к единице, во всем диапазоне частот. Вместе с тем нормально, если она принимает малые значения в точках антирезонанса или в тех узлах конструкции, где вибрационный отклик очень слаб (рис. 12).

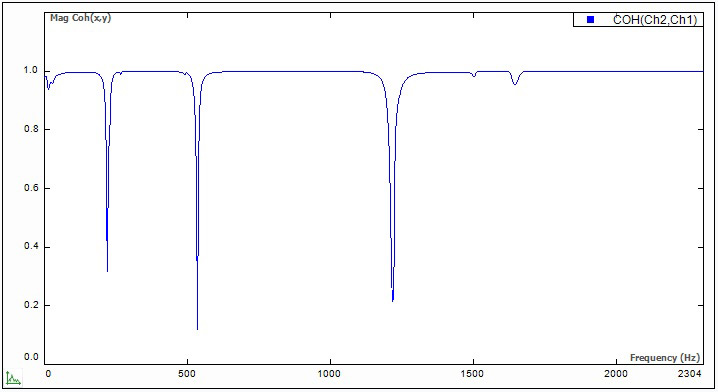
Рис. 12. Функция когерентности показывает качество данных ЧПФ

Усреднение

Представление данных в частотной области рассчитывается обыкновенно по одной временной выборке. В каждой такой выборке содержится некоторый случайный шум, способный маскировать истинные резонансные частоты и собственные формы колебаний. Если усреднить данные по нескольким выборкам, можно снизить уровень некоррелированного случайного шума. При этом необходимо отметить, что усреднение не влияет на приборный шум. К сигналам следует применять линейное усреднение с приданием одинакового веса всем выборкам или усреднение с экспоненциальным взвешиванием, при котором последней выборке придается наибольший вес, а первой — наименьший. Преимущество усреднения заключается в том, что оно способствует ослаблению случайного шума и сглаживанию данных. Вообще говоря, усреднение в частотной области не устраняет фоновый шум, но дает лучшую оценку среднего значения в каждой точке по оси частот.

Примером может служить рис. 13, демонстрирующий результат усреднения случайного сигнала. На верхнем графике показан спектр по данным одного кадра, на среднем — после 10 усреднений, а на нижнем — после 40 усреднений. Чем больше усреднений, тем больше сглаживаются перепады между отдельными спектральными линиями.

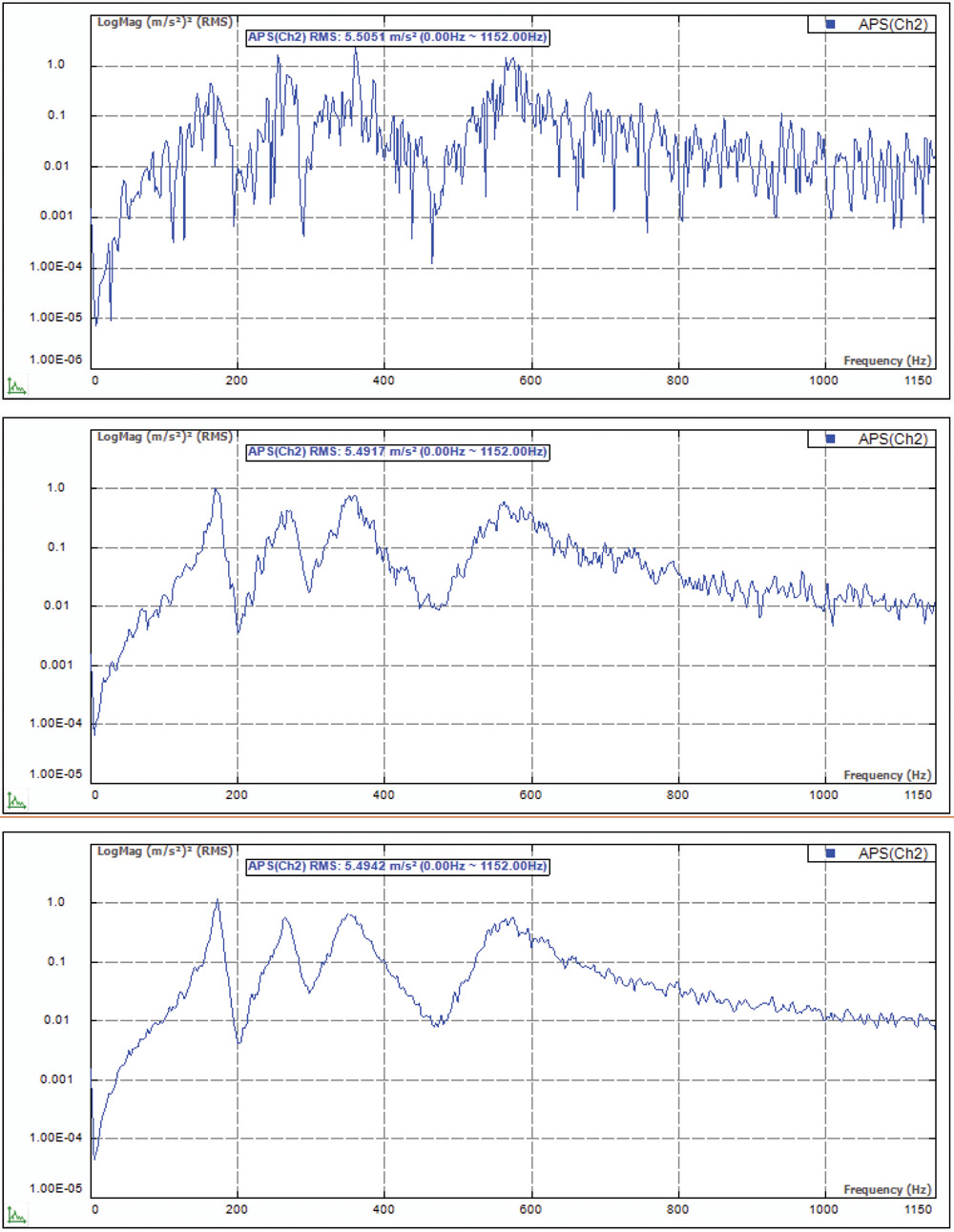
Рис. 13. Усреднение снижает уровень некоррелированного случайного шума, сглаживая спектр

Целесообразное количество усреднений для конкретного применения следует определять из инженерных соображений. Пользователю нужно учитывать случайность измеряемого сигнала, требуемое качество результатов и время регистрации каждого кадра. Общее практическое правило: делать 32–64 усреднения при испытаниях на вибростенде и 4–8 усреднений при испытаниях с использованием ударного молотка.

Синхрозапуск

Синхрозапуск (triggering) — это техника измерения, состоящая в том, что регистрация данных на анализаторе откладывается до наступления некоторого события, например удара молотком. Для этого можно настроить анализатор так, чтобы регистрация и обработка данных не начинались, пока на входном канале не будет обнаружен некоторый уровень напряжения. После приведения схемы синхрозапуска в состояние готовности анализатор инициализируется и ожидает ударного воздействия, чтобы начать регистрацию данных с этого момента. Синхрозапуск можно настроить таким образом, чтобы после каждого срабатывания схема снова автоматически приводилась в состояние готовности и можно было бы произвести несколько последовательных ударов молотком и усреднить отклики на них, не взаимодействуя с анализатором сигналов. Необходимо проследить за тем, чтобы не терялось начало выборки данных до момента срабатывания синхрозапуска — для этого можно установить отрицательный интервал предзапуска (pre-trigger). Этот параметр позволяет зарегистрировать несколько отсчетов данных, поступивших непосредственно перед сигналом синхрозапуска. В таком случае сигналограмма удара будет целиком содержаться в одном кадре.

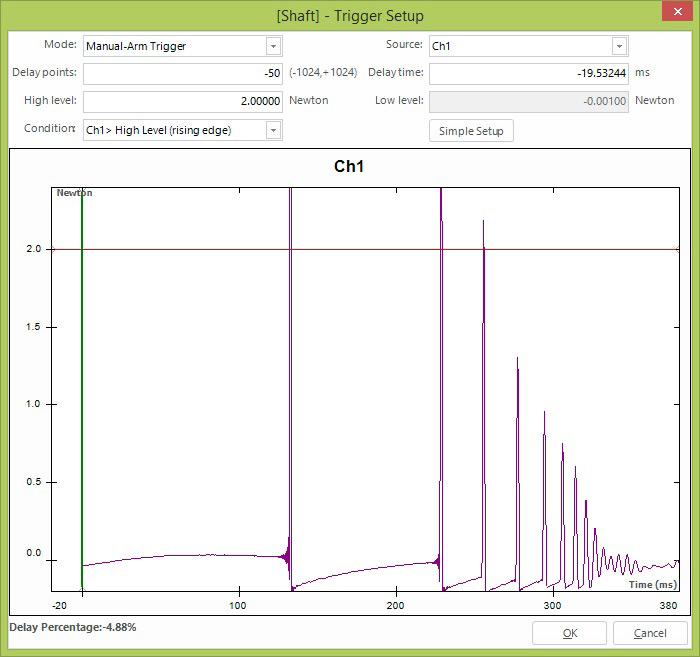
Рис. 14. Программный интерфейс для настройки синхрозапуска

В случае модального вибростенда синхросигнал берется с источника сигнала возбуждения, чтобы начало регистрации данных было синхронизировано с таким сигналом. Это чрезвычайно важно — особенно при использовании импульсных и случайно-периодических сигналов возбуждения (например, случайно-импульсных и псевдослучайных). Смысл в том, чтобы зарегистрировать все сигналы в одном временном интервале и сохранить их периодические характеристики.

Применение оконных функций

Оконные функции необходимы при расчете БПФ в случаях, когда измеренный сигнал не является периодическим в пределах временно́й выборки. В общем случае она нужна при использовании вибростенда для возбуждения вибрации в системе широкополосным случайным шумом. При вычислении БПФ от непериодического сигнала возникает явление растекания (leakage) энергии сигнала по широкому диапазону частот, тогда как периодический сигнал того же характера был бы сосредоточен в узком диапазоне.

Поскольку большинство сигналов не являются периодическими в пределах временно́й выборки, приходится применять оконные функции, чтобы придать сигналам периодическую форму и устранить растекание.

Оконная функция в точности равна нулю в начале и конце каждой выборки данных, а между этими точками имеет ту или иную специальную форму в зависимости от типа окна. Временну́ю выборку данных умножают на эту функцию, в результате сигнал становится периодическим. Чтобы правильно восстановить уровень сигнала БПФ после применения оконной функции, необходимо также умножить результат на специальный весовой коэффициент оконной функции. На рис. 15 показан результат применения прямоугольной оконной функции к чистому синусоидальному сигналу. На левом верхнем графике представлен синусоидальный сигнал, который является в точности периодическим в пределах временной выборки и к которому не применена оконная функция. БПФ этого сигнала (слева внизу) не имеет признаков растекания, то есть спектр его узок, а пиковая амплитуда равна единице, что соответствует амплитуде данного синусоидального сигнала во временной области. На среднем верхнем графике показан синусоидальный сигнал, не являющийся периодическим в пределах временной выборки, что приводит к растеканию БПФ в частотной области (внизу в середине). При растекании высота пика снижается, а его основание уширяется. Если применить окно Хэннинга (справа вверху), растекание сигнала БПФ уменьшается (справа внизу), а амплитуда пика принимает правильное значение, хотя уширение пика полностью не исчезает.

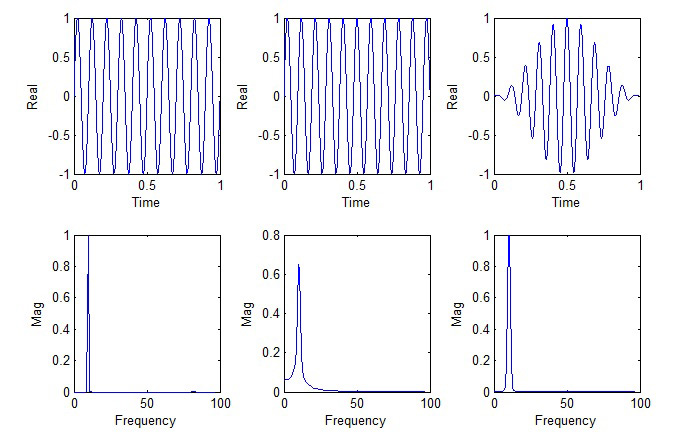
Рис. 15. Прямоугольное окно (справа) ослабляет эффект растекания (в середине)

Суть эффекта уширения легко понять в случае синусоидальных сигналов, но он влияет и на измерение сигналов других форм. На рис. 16 показана амплитудно-фазовая частотная характеристика (с примененной к ней оконной функцией Хэннинга и без таковой). Здесь эффект растекание энергии наиболее явственен в месте нахождения глубоких впадин. Кроме того, растекание может приводить к амплитудным, а следовательно, и частотным ошибкам, как и в случае синусоидальных сигналов.

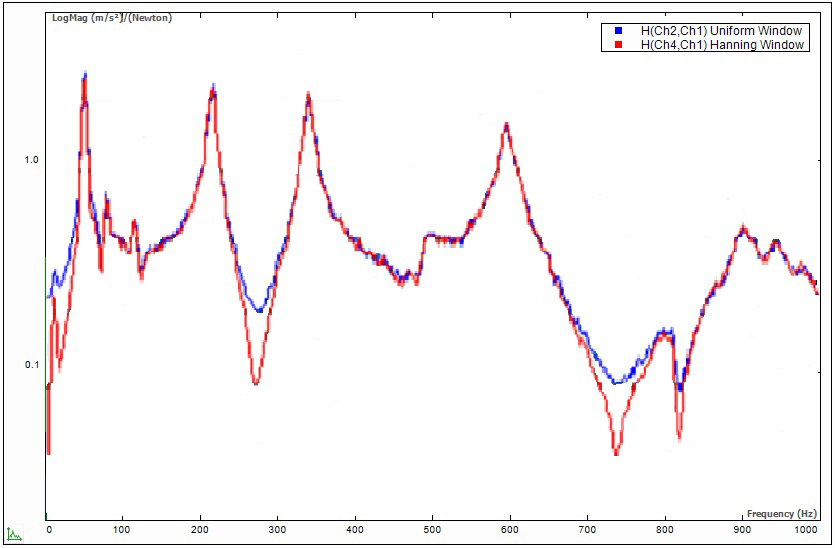
Рис. 16. Амплитудно-фазовая частотная характеристика с примененной к ней оконной функцией и без таковой

Когда вибрация в конструкции возбуждается с помощью ударного молотка, длительность временной выборки можно отрегулировать так, чтобы измеренный отклик полностью затухал в ее пределах. В этом случае, поскольку сигнал начинается и заканчивается нулевым значением, оконная функция не нужна, что даст наиболее точные значения амплитуды и коэффициента демпфирования. Если конструкция со слабым демпфированием продолжает вибрировать на протяжении очень длительного промежутка времени или если присутствует фоновый шум, можно применить специальную прямоугольно-экспоненциальную (force/exponential) оконную функцию. Эта оконная функция (рис. 17) состоит из двух частей: прямоугольного окна в начале временной выборки и следующего за ним до конца выборки экспоненциального окна. Прямоугольное окно имеет паузу в начале, которая призвана отсечь приборный шум до удара молотка. Пользователь может задать длительность этой паузы таким образом, чтобы она совпадала с интервалом предзапуска, и таким образом уменьшить влияние шума. Экспоненциальное окно, длящееся до конца временно́й выборки, задает экспоненциальное затухание вибрационного отклика конструкции до нуля к концу выборки, чтобы получить гарантированно периодический сигнал. Следует отметить, что при этом смещается вверх оценка коэффициента демпфирования конструкции, так как данная оконная функция сообщает сигналам ускоренное искусственное затухание.

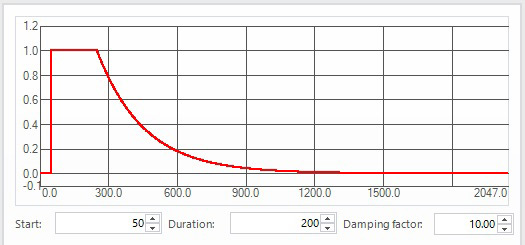
Рис. 17. Прямоугольно-экспоненциальная оконная функция, используемая при модальном анализе с возбуждением вибрации ударным молотком

На рис. 18 вверху показана сигналограмма отклика конструкции во временной области без применения оконной функции. Обратите внимание, что к концу записи вибрация конструкции затухает не полностью. На нижнем графике показан результат применения прямоугольно-экспоненциального окна, которое принудительно ослабляет до нуля сигнал вибрационного отклика конструкции к концу записи.

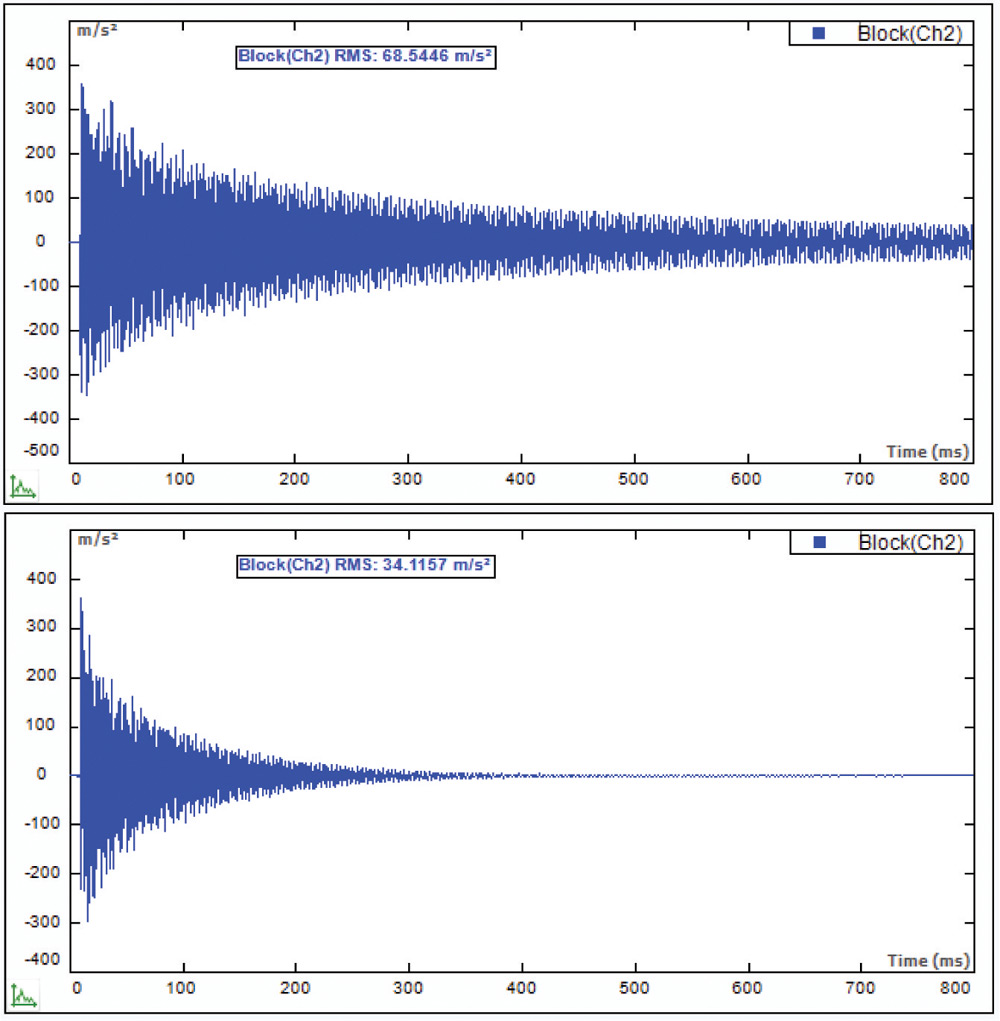
Рис. 18. Сигналограмма вибрационного отклика конструкции со слабым демпфированием (вверху) и она же с применением прямоугольно-экспоненциального окна (внизу)

Повышение разрешения при измерении

Один из важных факторов при выполнении измерений в ходе модальных испытаний — разрешение по частоте, или наименьшее расстояние между спектральными линиями. Когда собственные частоты близки друг к другу, может потребоваться более высокое разрешение по частоте, чтобы корректно измерить частоту и коэффициент демпфирования двух пиков. Есть два способа повысить разрешение по частоте: взять выборку большего размера или применить увеличение БПФ. Разрешение по частоте определяется количеством точек во временно́й выборке; чем больше точек, тем больше частотных линий будет в спектре БПФ. Таким образом, разрешение по частоте можно повысить, увеличив количество точек во временно́й выборке. Недостаток данного способа в том, что он требует увеличения длительности регистрации данных, а значит, и общей длительности измерения. Это особенно заметно, когда диапазон частот очень узок, например, менее 50Гц.

Второй способ повысить разрешение по частоте — применить увеличение БПФ. Для этого по особому алгоритму рассчитывают спектр в диапазоне частот, не начинающемся с нулевой частоты, в отличие от стандартных спектров основной полосы, которые обычно используют в прочих случаях. В динамическом анализаторе сигналов можно задать среднюю частоту, количество спектральных линий и диапазон частот. Спектральные линии распределяются в промежутке между нижней и верхней частотой диапазона с центром на заданной средней частоте. Результирующий спектр частотно-ведомого отклика (frequency-following response) имеет очень высокое разрешение по частоте в сравнении с обычным БПФ-анализом.

На рис. 19 даны для сравнения графики частотной передаточной функции конструкции с разным разрешением по частоте. Первое измерение выполнено с 400 спектральными линиями. Широкий горб вблизи 90 Гц представляет, вероятно, пару сильно связанных собственных форм колебаний. Ввиду тесной связи между этими двумя собственными формами точно определить амплитуду и коэффициент демпфирования при настолько низком разрешении по частоте не представляется возможным. Для второго измерения количество спектральных линий было увеличено до 1600. Теперь можно четко различить два близко расположенных друг к другу пика. В третьем измерении, где использовалось увеличение БПФ (диапазон частот 300 Гц, средняя частота 200 Гц), достигнуто наивысшее разрешение по частоте из всех трех измерений. Обратите внимание, что результат измерения с увеличением БПФ не содержит данных на частотах ниже 50 и выше 350 Гц, поскольку этот спектр не является спектром основной полосы.

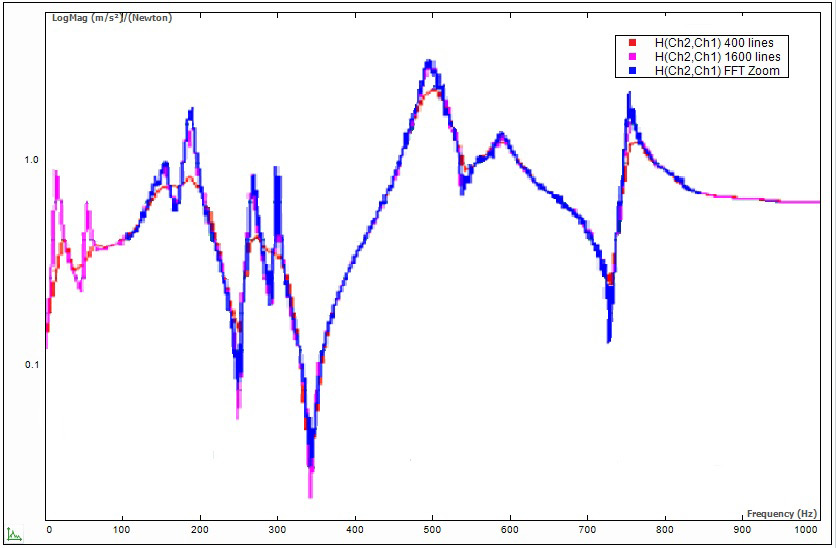
Рис. 19. Повышение разрешения по частоте: сравнение спектров с разрешением 400 и 1600 линий, а также с увеличением БПФ

Качество сигнала: перегрузка и двойной удар

Качество сигнала — важный фактор при регистрации данных для модального анализа. Если не контролировать качество регистрируемых данных, результаты модального анализа могут оказаться ошибочными или некорректными. Первый шаг в оценке качества сигнала — контроль функции когерентности. Если она имеет ненадлежащий вид, следует принять меры к ее улучшению, прежде чем регистрировать данные в окончательном виде.

Другие факторы, влияющие на качество сигнала, — перегрузка и двойной удар молотка. Перегрузка происходит, когда сигнал с акселерометра или тензодатчика ударного молотка выходит за пределы диапазона напряжений входного канала динамического анализатора сигналов. Например, если верхний предел диапазона напряжений входного канала анализатора установлен равным 1,0 В, и при сильном ударе молотком тензодатчик вырабатывает напряжение 1,5 В, результатом станет перегрузка входного канала. В большинстве анализаторов сигналов предусмотрена сигнализация о перегрузке. Все данные, полученные в ходе измерения с перегрузкой, будут некорректными, и их следует отбросить, а испытание повторить для получения новых данных. Чтобы избежать перегрузки, можно уменьшить силу удара по конструкции, расширить диапазон напряжений входного канала анализатора либо выбрать менее чувствительный акселерометр или ударный молоток (то есть встроенный тензодатчик). Большинство динамических анализаторов сигналов способно обнаруживать перегрузку и предупреждать пользователя, предоставляя ему возможность отбросить некорректные данные, чтобы они не повлияли на усредненные сигналы.

Двойной удар при испытаниях с ударным молотком — это ситуация, когда молоток ударяет по конструкции, а та отскакивает и ударяет по наконечнику молотка. Второй удар может следовать через считаные миллисекунды после первого, и его легко не заметить на графиках. Данные, полученные в ходе испытания с двойным ударом, также некорректны, поэтому их следует отбросить, а испытание повторить. Распознать двойной удар можно, просмотрев тензограмму воздействия ударного молотка в режиме увеличения на этапе регистрации данных.

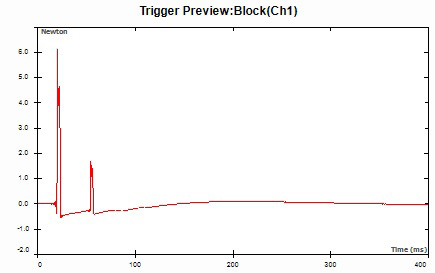
Рис. 20. Двойной удар молотка, ухудшающий качество результатов модального анализа, можно распознать на тензограмме

Маркировка данных и автоинкремент

Для того чтобы собрать данные для модального анализа, необходимо измерить вибрационный отклик во всех точках исследуемой конструкции. Обычно в результате получается довольно объемный набор данных. Собранные сведения импортируются в программное обеспечение для модального анализа, и каждому измерительному сигналу сопоставляется точка и направление на конечноэлементной модели исследуемой конструкции. Такое сопоставление является нетривиальной задачей и играет ключевую роль. Во многих динамических анализаторах сигналов имеется функция автоматической маркировки каждой точки.

Эта маркировка содержит «данные о степенях свободы» (DOF) — номер точки и направление измерительного датчика. Направление отсчитывается в определенной системе координат — декартовой (+x, +y, +z, –x, –y, или –z). По этой информации программное обеспечение для модального анализа может автоматически сопоставить измерительные данные соответствующей точке конструкции. Автоинкремент — это функция автоматического перехода к следующей точке и/или следующему направлению по окончании каждого измерения. Данные о степенях свободы можно всегда ввести вручную или исправить в ходе испытания. Собрав все необходимые данные о степенях свободы, получившийся набор можно сохранить и передать в программное обеспечение для модального анализа, где будет проходить следующий этап работы.

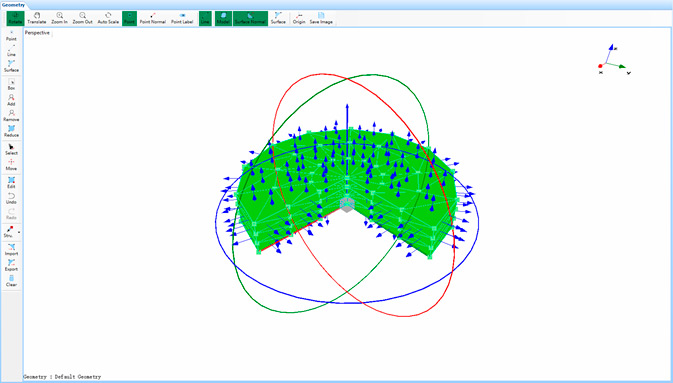
Рис. 21. Задание степеней свободы модели изделия

Экспорт данных

После того как полученные при измерении результаты будут зарегистрированы и весь получившийся набор данных будет сохранен, необходимо экспортировать данные в формате, который поддерживается программным обеспечением для модального анализа. Таким образом, от динамического анализатора сигналов требуется способность сохранять или экспортировать данные в формате, непосредственно читаемом таким программным обеспечением. Поскольку количество данных может быть очень велико, редактировать файл данных вручную неудобно и неэффективно. В большинстве динамических анализаторов сигналов предусмотрена возможность экспорта данных в ряде популярных форматов, поддерживаемых многими распространенными программными пакетами для модального анализа. Одним из таких форматов является UFF (Universal File Format — «универсальный формат файла»). Он широко используется для передачи данных между большинством программных пакетов, а также из динамического анализатора сигналов в программное обеспечение для модального и конечноэлементного анализа.

Модальный анализ

Когда данные собраны и импортированы в программное обеспечение для модального анализа, следующий шаг — определить по этим данным модальные параметры, в том числе собственные частоты, коэффициенты демпфирования и собственные формы колебаний. Для этого нужно построить геометрическую модель исследуемой конструкции. Собственные формы колебаний визуализируются в виде анимации геометрической модели. Есть несколько популярных программных пакетов для модального анализа, у каждого из них свой собственный интерфейс, но все они работают по одному и тому же принципу, который описывается ниже.

Построение геометрической модели

Геометрическую модель конструкции можно построить до или после регистрации данных для модального анализа. Геометрическая модель состоит из точек, линий и поверхностей, расположение которых повторяет форму конструкции. В большинстве программных пакетов для модального анализа есть инструменты для создания этих геометрических элементов, а также обычно имеется библиотека компонентов, таких как балка, пластина, куб, цилиндр или сфера. Пользуясь этими инструментами, можно построить геометрическую модель любой конструкции.

Простые элементы (компоненты) можно соединять друг с другом, составляя из них весьма замысловатые структуры. Модель может быть очень простой или очень сложной в зависимости от необходимого уровня точности результатов анализа. Например, балку можно представить всего несколькими точками, соединенными линиями, — этого достаточно для визуализации первых нескольких собственных форм колебаний. Но чтобы точно смоделировать сложную конструкцию наподобие спутниковой тарелки, потребуется гораздо больше точек и других элементов.

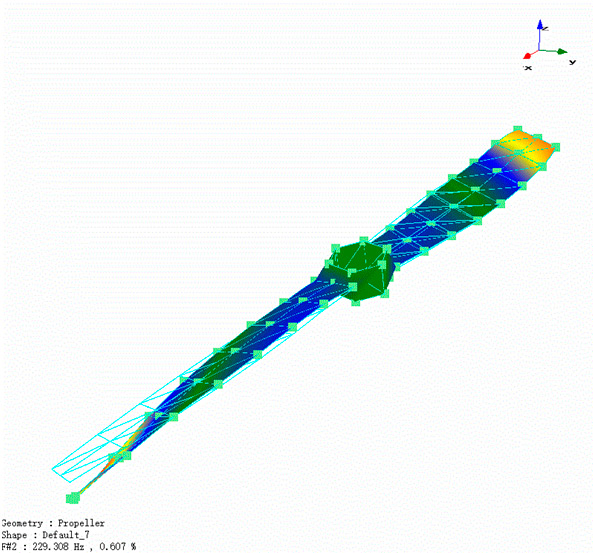
Рис. 22. Простая модель винта самолета (сверху) и сложная модель автомобиля (снизу)

При построении геометрической модели необходимо учитывать количество собственных форм колебаний. Собственные формы, связанные с более низкими резонансными частотами, обычно имеют более простой вид, и для их адекватного представления достаточно нескольких точек. Более высокочастотные собственные формы могут выглядеть сложнее и требовать более высокого разрешения модели с бо́льшим числом точек.

Сопоставление измерительных данных геометрической модели

Следующий шаг — сопоставить измерительные данные геометрической модели. Модель состоит из точек, соединенных линиями, а они, в свою очередь, могут быть соединены поверхностями. Это те точки, в которых измерялся вибрационный отклик конструкции. Измерительные данные сопоставляют точкам исследуемой конструкции и направлениям перемещения. В составе программного обеспечения для модального анализа предусмотрен инструмент для сопоставления данных ЧПФ точкам конструкции. Эту задачу выполняют вручную, выбрав точки и направления на модели, или автоматически по меткам степеней свободы, которыми снабжены измерительные данные.

Данные измерения ЧПФ

Описанный выше процесс упрощается при использовании функций маркировки данных и автоинкремента в динамическом анализаторе данных. Как правило, геометрическая модель строится таким образом, что все точки модели соответствуют точкам измерения на исследуемой конструкции. Большинство программных пакетов в этом случае может автоматически считывать метки степеней свободы (DOF) и, пользуясь ими, сопоставлять измерительные данные точкам и направлениям.

Бывает так, что не для каждой точки и направления на исследуемой конструкции существует измеренная ЧПФ. Программное обеспечение для модального анализа способно воссоздавать недостающие ЧПФ путем интерполяции между точками и направлениями, в которых произведены измерения. Пусть, например, ЧПФ на балке измерялась в шести точках в положительном направлении оси z, а геометрическая модель состоит из 10 точек — по одной дополнительной точке между каждой парой точек измерения. Тогда программное обеспечение рассчитает данные в промежуточных точках путем интерполяции измерительных данных, полученных в расположенных по соседству точках. В результате модель будет выглядеть более гладкой.

Определение модальных параметров

Ключевой этап модального анализа — определение модальных параметров исследуемой конструкции. Если конструкция имеет лишь небольшое количество далеко отстоящих друг от друга резонансных частот, это можно будет сделать простым способом, но если несколько собственных частот в спектре ЧПФ расположены близко друг к другу или повторяются, определить искомые параметры будет сложнее. Еще один параметр, представляющий интерес, — коэффициент демпфирования на каждой собственной частоте, который связан с остротой резонансного пика.

Любое программное обеспечение для модального анализа имеет в своем составе множество инструментов для определения собственных частот и коэффициентов демпфирования по данным измерения ЧПФ. В основу этих инструментов положены разные методы — с одной (SDOF) или несколькими (MDOF) степенями свободы, работающие во временной или частотной области, использующие один или несколько опорных сигналов. Один из простых методов с одной степенью свободы — квадратурный метод, при котором анализируется мнимая часть данных ЧПФ для поиска пика. В окрестности собственной частоты мнимая часть ЧПФ обычно выглядит как пик, если ЧПФ представлена в виде зависимости виброускорения от вынуждающей силы. На собственную форму колебаний указывает положительный или отрицательный пик (рис. 23).

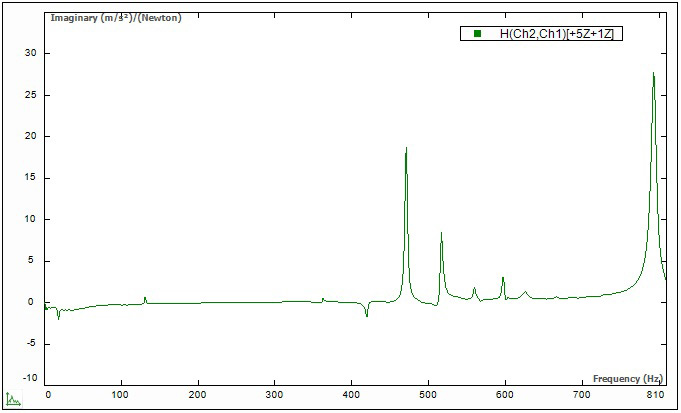
Рис. 23. Результаты измерения мнимой части частотной передаточной функции балки (зависимости виброускорения от вынуждающей силы)

В общем случае для определения каждой собственной формы по набору данных измерения ЧПФ используют аппроксимацию кривыми. При аппроксимации учитывается эффект связи для всех собственных форм в рассматриваемой полосе частот, даже если собственные частоты сильно связаны или вовсе повторяются. Ее также применяют в случае сильного демпфирования на собственной частоте, когда местоположение пика не является наилучшей оценкой значения собственной частоты. Любой метод аппроксимации заключается в подборе полюсной математической модели (задаваемой собственными частотами и коэффициентами демпфирования), наилучшим образом соответствующей имеющимся данным измерения ЧПФ в некоторой полосе частот. Модальные параметры из подобранной модели сохраняются и используются для дальнейшей оценки остатков.

После определения собственных частот и коэффициентов демпфирования программное обеспечение выполнит еще один шаг аппроксимации для оценки остатков (определения собственных форм колебаний) по всему набору данных измерения ЧПФ. Собственная форма колебаний определяется амплитудой и фазой ЧПФ на собственной частоте для каждой степени свободы (точки и направления) исследуемой конструкции.

Интерпретация результатов

Последний шаг — интерпретация результатов. Теперь можно визуализировать собственные формы колебаний на геометрической модели путем анимации. Для визуализации может быть выбрана любая собственная форма колебаний с определенными для нее собственной частотой и коэффициентом демпфирования. Последовательность анимации такова: геометрическая модель из недеформированного положения деформируется с заданным шагом до максимального положительного отклонения, затем, пройдя через исходное положение, деформируется в обратном направлении до максимального отрицательного отклонения и далее возвращается в исходное положение. Этот процесс циклически повторяется. Амплитуду анимированных колебаний можно увеличить или уменьшить, чтобы четче разглядеть исследуемую собственную форму. Анимированную геометрическую модель можно одновременно вращать вокруг своей оси — это позволяет рассмотреть собственную форму под наилучшим углом зрения. Есть также множество графических инструментов, помогающих визуализировать собственные формы колебаний. Один из таких инструментов — цветовая карта, позволяющая закодировать цветом амплитуду деформаций для выбранной собственной формы. Можно также представлять деформации на геометрической модели векторами, направленными из недеформированного положения в деформированное. Все эти инструменты помогают пользователю понять характер деформаций при каждой собственной форме колебаний.

Рис. 24. Пример анимации вибрации геометрической модели исследуемой конструкции

Пример из практики

В следующем примере рассматривается регистрация данных и модальный анализ при испытаниях глушителя с выхлопной трубой. Конструкция крепится к раме эластичными жгутами, чтобы граничным условием была свобода с обоих концов. Точки измерения располагаются в соответствии с геометрической моделью, построенной в программном обеспечении для модального анализа.

Средствами возбуждения и регистрации вибрационного отклика служат ударный молоток и акселерометр. Акселерометр крепится в одной точке измерения воском, а воздействие ударным молотком осуществляется последовательно в разных точках для каждого измерения ЧПФ. Данные регистрируются с помощью динамического анализатора сигналов Crystal Instruments с программным обеспечением для динамического анализа сигналов EDM. По итогам нескольких тестовых измерений, согласно которым первая собственная частота находится в окрестности 100 Гц, диапазон частот анализа ограничивается 500 Гц. Сигналограммы вынуждающей силы и вибрационного отклика показывают, что вибрация затухает менее чем за 200 мс, поэтому длительность временно́й выборки устанавливается равной 400 мс. Режим измерения — 4 линейных усреднения, синхрозапуск по входному сигналу с интервалом предзапуска для регистрации импульсов.

Интерфейс программного обеспечения для динамического анализа сигналов настраивается для отображения измеренной ЧПФ, функции когерентности и сигналограмм вынуждающей силы и виброускорения. Эти данные используются для контроля качества регистрируемых данных.

В окне модальных координат отображаются текущий идентификационный номер точки измерения и направление измерения. Номер точки автоматически обновляется с использованием функции автоинкремента. На экране может быть отображен индикатор статуса каналов (Channel Status), показывающий уровень напряжения на входных каналах и факт перегрузки.

После того как все параметры настроены и проверены, можно регистрировать данные ЧПФ. В каждой точке измерения на исследуемой конструкции усредняются данные, полученные от четырех ударов молотком. Результирующие 30 усредненных сигналов ЧПФ измеряются и сохраняются на диск в формате UFF, а затем импортируются в программное обеспечение для модального анализа EDM Modal, чтобы определить модальные параметры.

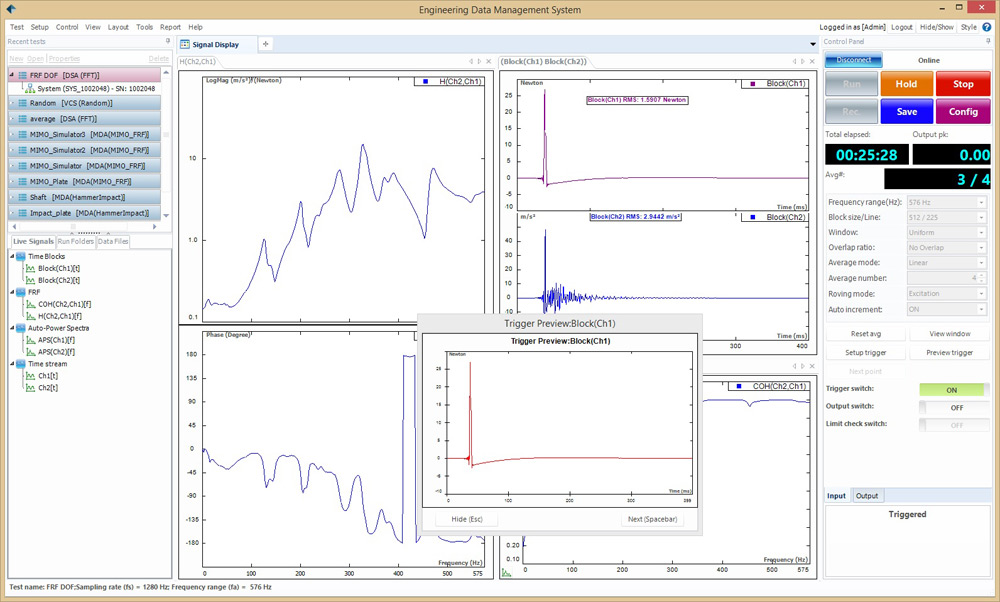
Рис. 25. Интерфейс программного обеспечения компании Crystal Instruments для модального анализа и испытаний

В программном обеспечении EDM Modal построена геометрическая модель, показанная на рис. 26. Она повторяет фактическую форму конструкции. Геометрическая модель сформирована из точек, линий и поверхностей. Она копирует размеры и форму реальной конструкции. Модель не только помогает задавать точки измерения, но и может использоваться для визуализации собственных форм колебаний в анимированном виде.

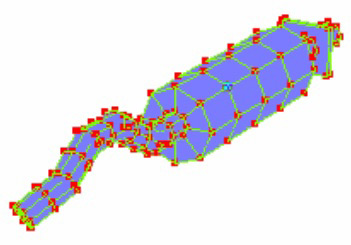
Рис. 26. Геометрическая модель глушителя с выхлопной трубой

По меткам данных (точка и направление), сохраненным программным обеспечением Crystal Instruments для динамического анализа сигналов, измерительные данные автоматически сопоставляются точкам и направлениям на исследуемой конструкции. С помощью инструментов для аппроксимации кривыми определяются модальные параметры, в том числе собственные частоты, коэффициенты демпфирования и собственные формы колебаний. Одна из собственных форм колебаний показана на рис. 27. Вид сбоку (см. правый нижний рисунок) позволяет наилучшим образом разглядеть эту собственную форму, связанную с изгибом. Она напоминает букву S, ее максимальные отклонения наблюдаются на отметках 1/4 и 3/4 длины, а нулевое отклонение — в окрестности середины. Это классическая собственная форма колебаний конструкций типа балки. Отсюда можно видеть, что теоретические предсказания вибрационного отклика простых конструкций можно в определенной мере распространить и на более сложные случаи.

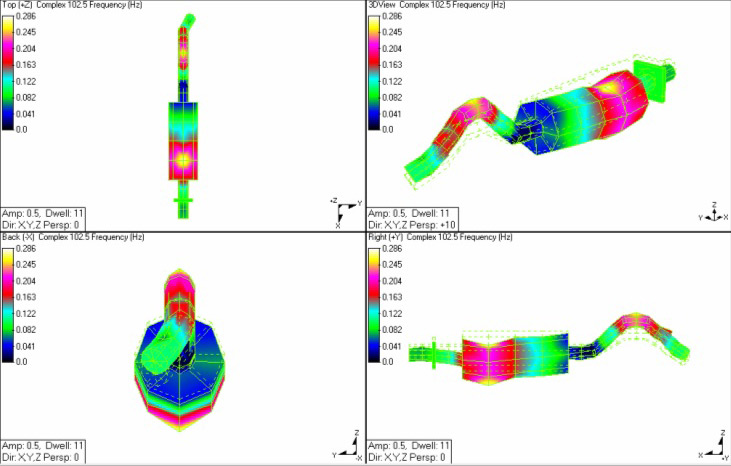
Рис. 27. Первая собственная форма колебаний, визуализированная с использованием цветовой карты

По этим результатом можно определить критически важные точки конструкции, в которых с большой вероятностью будет наблюдаться высокий уровень вибрации. Данные о собственной форме колебаний представлены в относительном выражении. В предположении линейности амплитуда вибрации пропорциональна уровню возбуждения. При необходимости конструкцию корректируют, изменив ее поперечное сечение, добавив элементы жесткости или покрыв ее демпфирующими материалами для изменения модальных параметров. Исходя из данных модального анализа, можно, например, рассмотреть варианты выбора других точек крепления глушителя к транспортному средству. Во многих случаях подобный анализ начинают с простой модели, чтобы выявить проблемные области. Затем, если затраты времени и усилий оправданы, можно построить усовершенствованную модель с более точными измерениями.

Выводы

Модальный анализ находит широкое применение в качестве средства решения инженерных задач, связанных с вибрацией. Он позволяет определять модальные параметры исследуемой конструкции, в частности собственные частоты, коэффициенты демпфирования и собственные формы колебаний. В программном обеспечении для имитационного моделирования (например, на основе метода конечноэлементного анализа) используется математическая модель конструкции, а при экспериментальном модальном анализе оперируют данными измерений на реальной конструкции. Экспериментальный модальный анализ обычно выполняется в два этапа. На первом этапе регистрируются данные для определения частотных передаточных функций, а на втором определяются модальные параметры и визуализируются собственные формы колебаний на геометрической модели конструкции. Исходя из определенных по итогам анализа собственных частот, коэффициентов демпфирования и собственных форм колебаний, можно внести изменения в конструкцию для подавления вибрации или изменить характер возбуждения, чтобы избежать вхождения в резонанс.